0bfusc8 much (re497)
We are given a rather large binary (1.8MB). Attempting to decompile it using IDA does not work, also there are too many nodes for IDA to render the graph view.
Analysing the program behaviour
While this looks daunting, we can start off by observing certain patterns in the obfuscated binary. A typical compiler would not generate such a large binary, so we can assume that there would be some common code patterns generated by the obfuscation pass.
Firstly, we can see at the start of the main function, there is a call to memset followed by scanf referencing an address on the stack. From this we can deduce that the flag is 71 bytes long.
char* input;
memset(input, 0, 0x47);
scanf("%s", input);
Following the instructions, we can see that the first byte of our input is retrieved and the cube of the value is stored on the stack.
movsx ecx, [rbp+input]
movsx r8d, [rbp+input]
imul ecx, r8d
movsx r8d, [rbp+input]
imul ecx, r8d
...
mov [rbp+var_78], ecx
Then, the program branches off depending on the result of (c * c * c) % 1, where c is the first byte of our input.
After which, we start seeing repeating patterns of instructions. There will always be a few lines of instructions, then jump to somewhere else. For example,
; a few lines of doing something
mov rax, rsp
add rax, 0FFFFFFFFFFFFFFF0h
mov rsp, rax
mov [rbp+var_1C8], rax
; performs some checks to determine where to branch to
mov al, 1
test al, al
jnz loc_401719
jmp $+5
xor eax, eax
mov cl, al
test cl, cl
jnz loc_401A03
jmp $+5
jmp groups
The jmp instructions exist in the following forms, attempting to look like they are conditional jumps but actually are unconditional jumps.
In the following example, the first jnz would never happen, and the second one would always be taken.
mov al, 1
test al, al
jnz somewhere
jmp $+5 ; just goes to the next instruction
xor eax, eax
mov cl, al
test cl, cl
jnz somewhere
jmp $+5
Popping off the stack
In an earlier example, we encountered this set of instructions, which turned out to be very common in the program.
mov rax, rsp
add rax, 0FFFFFFFFFFFFFFF0h
mov rsp, rax
mov [rbp+var_1C8], rax
In essence, it decrements the stack pointer, then stores it somewhere on the stack, effectively pushing something onto the stack.
In other parts of the program, we would see something like the following.
xor eax, eax
mov ecx, eax
sub ecx, 0
mov edx, eax
sub edx, 0
sub ecx, edx
sub eax, ecx
; after doing something to eax, which actually is nothing, if you look at the instructions
mov rcx, [rbp+var_1C8]
mov [rcx], eax
Notice the last 2 lines, the stack pointer stored earlier was retrieved, and the program stores a value into that address.
The main effect of this is we cannot just rename a stack variable and step through the code to see what happens to it, because the location of that variable will keep changing. For example, the following code just moves a value into a different location on the stack.
; reads from somewhere
xor eax, eax
mov rcx, [rbp+var_218]
mov edx, [rcx]
; actually this does nothing, since eax and esi are 0
; eax = -edx
mov esi, eax
sub esi, 0
sub edx, esi
sub eax, edx
; stores it elsewhere
mov rdi, [rbp+var_208]
mov [rdi], eax
jmp loc_401947
Reversing the code checking algorithm
Now that we got a clearer understanding of the binary, knowing the repetitive code patterns, perhaps it is time to write a “deobfuscator” to see the actual operations performed on our input. Actually nope, I didn’t do that.
I decided to go the tedious way of stepping through these instructions in GDB. But since I know that a lot of the instructions are dead code, I can quickly skip through them and see what is important.
Knowing the flag format is hackim19{...}, I entered the first few correct characters and started to follow the program’s path. While doing this, I need to keep close attention to the variables, since as mentioned earlier their location on the stack will keep changing. Every time they change location, they may be added with or multiplied by some constant, so one mistake will mean I have to start again.
After a few painful minutes, I managed to reach the part where the next character of the input is retrieved. But in order to get there, we need [rbp+var_4D8] to be equal to 0.
mov rax, [rbp+var_4D8]
cmp dword ptr [rax], 0
jnz loc_40A770
movsx eax, byte ptr [rbp+input+2]
Here is what happened to [rbp+var_4D8], which is stored with the value of 0xf3d38 - [rbp+var_4F8].
; reads from var_4F8
xor eax, eax
mov rcx, [rbp+var_4F8]
mov edx, [rcx]
; eax = [rbp+var_4F8] - 998712
mov esi, eax
sub esi, 0F3D38h
sub edx, esi
sub eax, edx
; stores it in rbp + var_4D8
mov rdi, [rbp+var_4D8]
mov [rdi], eax
jmp loc_403B04
Ok, then what is [rbp+var_4F8]? It was $x^3 - 300x^2 + 29987x$, where $x$ is the first character of our input. In other words we need to satisfy the cubic equation of
And indeed, as the first character of our flag, the numeral value of h, 104, is one of the solutions to this equation.
Are the rest the same?
Now we can make a bold assumption that the rest of the characters of the flag are also validated by a cubic equation. To verify this assumption, I stepped through the instructions for checking the 3rd character (the program checks the 2nd character after the 3rd).
Turns out that it also needs to satisfy the same equation.
\[x^3 - 300x^2 + 29987x - 998712 = 0\]Definitely time to check the solutions to this equation, and yes they are the numeral values of h, a and c, the first 3 characters of our flag. Since the last coefficient, the constant value is the product of roots, the characters we want to find will just be the factors of that number.
Capture the Flag
Now we know what the program does. For every 3 consecutive characters, they need to be the factors of a certain constant value. So, what’s left is to retrieve these constant values and generate the flag.
For reference, here’s a screenshot of the list of cross references to our input. Note that each character is retrieved twice during the validation process, and they are read in the order of first, third, then second.
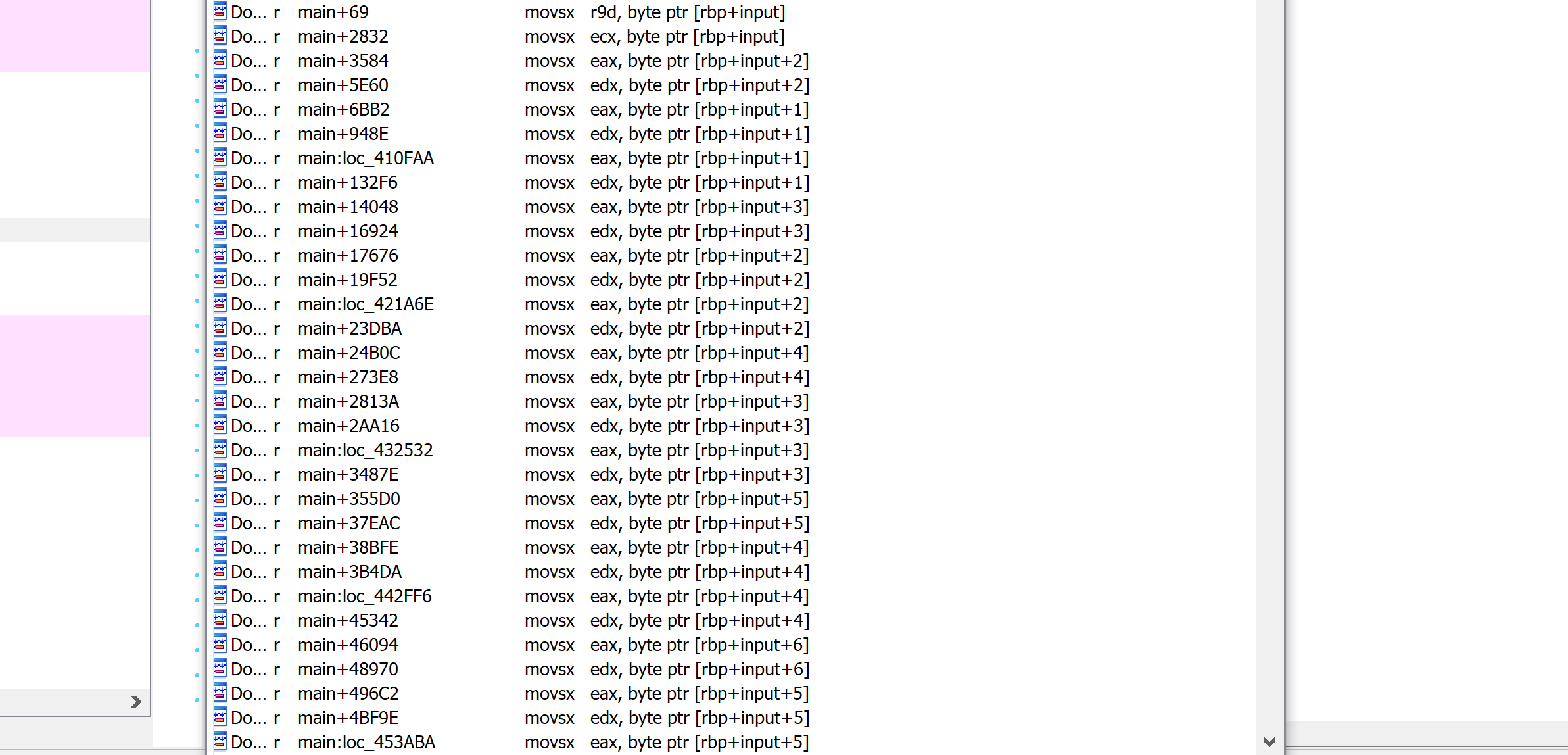
At the start, we found out that the flag consists of 71 characters. It is a large number, but the way this binary is obfuscated makes it that finding a way to automate getting the flag may not be a trivial task. (at least it would take more time to code such a solution than to retrieve the flag by hand)
However, it is very easy to get the constant values representing the flag. We just need to find xrefs to our input then scroll around in IDA. I then wrote a simple script to assist me in decoding the characters of the flag.
flag = "hac"
def prod(l):
return ord(l[-1]) * ord(l[-2])
while True:
p = int(raw_input(), 16)
flag += chr(p / prod(flag))
print flag
hackim19{Get_Hard_In_Dynamic_Reversing_ASAP_brace_me_when_you_trace_me}